Advanced D3: Layouts
Material based on Alexander Lex’s lecture, Scott Murray’s book and blocks by Mike Bostock
Layouts
Layouts make it easier to spatially arrange, shape and size elements representing data on the screen. While we’ve produced layouts ourselves already, we’ve only used simple position and size assignments that were directly driven by the data. And while these cover important classes of visualization techniques, there are more advanced techniques for different data types that are not as easily placed. Layouts are typically based on algorithms that define, e.g., where to put a node in a network visualization, or where to place a rectangle in a tree map. In this lecture we will learn how to use D3’s layout features to render such complex layouts.
D3 Layouts don’t actually draw things for us, rather they perform a data transformation that we can use to draw specific objects on the screen. Let’s start with a simple example, a pie chart.
A Pie Chart
Pie charts are a much criticized visualization technique as they have multiple weaknesses (but also strengths) compared to their alternatives. We’ll talk about those in class, but for now, we’ll draw a pie chart because it’s one of the simplest layouts we can do.
In the following example, we use the D3 pie layout to calculate the angles and the d3.arc function to calculate the arcs used for drawing the wedges.
See output in new page.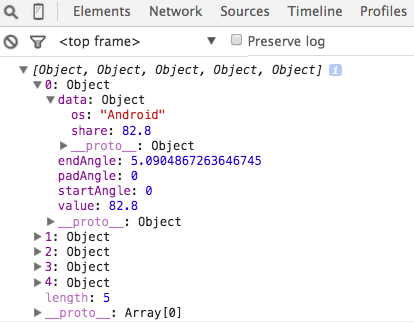
The interesting intermediate stages here are the values produced by the pie layout and the path drawn by the arc function. The pie layout produces a specific data object that we can use to bind to the DOM elements, shown on the right. We get an array with one object for each wedge. The first member of the object is data, which stores the raw data. We also have startAngle and endAngle (in radians).
The path that is generated by the arc function, is the second piece of information: M1.1634144591899855e-14,-190A190,190 0 1,1 -176.58002257840997,-70.13911623486732L0,0Z. This defines the actual path drawn.
A Force-Directed Graph Layout
We’ve mainly talked about tabular data up to this point. As we will soon learn, there are other data forms. A major other data form is the graph or network. Graphs describe relations between elements. The elements are usually referred to as nodes or vertices, the relationships as links or edges. A common, but not the only representation for graphs are node link diagrams, where nodes are often rendered as circles and edges as lines connecting the circles. There are many ways to lay the nodes in a graph out. We could have all nodes on a circle, or in a grid, or use some other method for laying them out. A common method is a force-directed layout. The idea behind a force directed layout is a physical model: the nodes repulse each other, while the edges are considered springs that pull each other close. The idea behind this is that as nodes that are tightly connected will be close to each other, i.e., form visible clusters, whereas nodes that are not connected are far from each other. The D3 implementation does not actually model this as springs, but as geometric constraints, but the mental model is still useful.
This happens in an iterative process, i.e., the forces for each node to each other node are calculated in a single step and the system is adjusted, then the next loop starts, etc. Eventually, the system will (hopefully) find an equilibrium. This is computationally expensive, as we will learn, but works fine for smaller graphs.
The following example illustrates a node-link diagram based on character co-occurrences in Les Miserables. It is based on the standard D3 force layout example.
The data is stored in a json file. Here is a sample of this file:
1 {
2 "nodes":[
3 {"name":"Myriel","group":1},
4 {"name":"Napoleon","group":1},
5 {"name":"Mlle.Baptistine","group":1},
6 {"name":"Mme.Magloire","group":1},
7 {"name":"CountessdeLo","group":1}
8 ],
9 "links":[
10 {"source":1,"target":0,"value":1}
11 {"source":2,"target":0,"value":8},
12 {"source":3,"target":0,"value":10},
13 {"source":3,"target":2,"value":6},
14 {"source":4,"target":0,"value":1}
15 ]
16 }The file contains a list of nodes, followed by a list of edges (links), a common format to store graph data. In the array of nodes, we have objects with the values name and group, the links array contain the edges that are defined via a source and target, which are indices into the nodes array (e.g., source 1 is Napoleon, traget 0 is Myriel).
First we will used D3’s XMLHttpRequest module (XHR), specifically the JSON method to load the data. Two things are important to note:
- Once the data is loaded it will be available in an object, just as we see it in the json file.
- The d3-request methods load asynchronously. That means that we’ll not get a return value from the loading function right away, but rather pass a function that is executed when the data loading is complete. The benefit of the asynchronous function is, of course, that other processes can continue, e.g., a user interface wouldn’t freeze up while a dataset is loaded.
We then use the force layout to calculate the initial positions and update them in “ticks”:
See output in new page.The layout uses a “cooling” factor that stops the iteration cycle.
Other Layouts
There are many other layouts that can be very valuable, for different types of data and use cases. We’ll revisit the layouts in class when we talk about the specific techniques they implement, but the principle is always the same: they take data and calculate derived data, which you then can use to position/scale graphical primitives on the canvas. You shouldn’t have a hard time understanding any of the other layout examples.

